本帖最后由 pig2 于 2014-11-14 23:39 编辑
问题导读
1.如何将乱序小球,使得三种颜色的球在一起?
2.你认为该如何编程实现实现矩阵乘法,并考虑当矩阵规模较大时的优化方法?

前言
本文要讲的两个问题:荷兰国旗和矩阵相乘之Strassen算法都跟分治法相关,故把这两个问题放到了一起。所谓分治,便是分而治之的意思,好比打战时面对敌人庞大的武装部队,采取避其主力,各个击破的策略。
有何问题,欢迎随时不吝指正,thanks。
荷兰国旗问题
题目描述
现有红白蓝三个不同颜色的小球,乱序排列在一起,请重新排列这些小球,使得红白蓝三色的同颜色的球在一起。这个问题之所以叫荷兰国旗,是因为我们可以将红白蓝三色小球想象成条状物,有序排列后正好组成荷兰国旗。如下图所示:
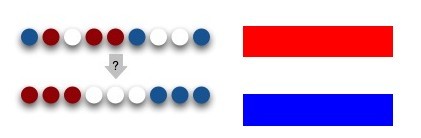
思路分析
初看此题,我们貌似除了暴力解决并无好的办法,但联想到我们所熟知的快速排序算法呢?我们知道,快速排序时基于分治模式处理的,对一个典型子数组A[p...r]排序的分治过程为三个步骤:
分解:A[p..r]被划分为俩个(可能空)的子数组A[p ..q-1]和A[q+1 ..r],使得A[p ..q-1].解决:通过递归调用快速排序,对子数组A[p ..q-1]和A[q+1 ..r]排序。合并。 也就是说,快速排序的主要思想便是依托于一个partition分治过程,每一趟排序的过程中,选取的主元都会把整个数组排列成一大一小的序列,继而递归排序完整个数组。
如下伪代码所示:
快速排序算法的关键是PARTITION过程,它对A[p..r]进行就地重排:
PARTITION(A, p, r)
- 1 x ← A[r]
- 2 i ← p - 1
- 3 for j ← p to r - 1
- 4 do if A[j] ≤ x
- 5 then i ← i + 1
- 6 exchange A A[j]
- 7 exchange A[i + 1] A[r]
- 8 return i + 1
继而递归完成整个排序过程:
- QUICKSORT(A, p, r)
- 1 if p
- 2 then q ← PARTITION(A, p, r) //关键
- 3 QUICKSORT(A, p, q - 1)
- 4 QUICKSORT(A, q + 1, r)
举个例子如下:i 指向数组头部前一个位置,j 指向数组头部元素,j 在前,i 在后,双双从左向右移动。
① j 指向元素2时,i 也指向元素2,2与2互换不变
- i p/j
- 2 8 7 1 3 5 6 4(主元)
② 于是j 继续后移,直到指向了1,1
复制代码
③ j 继续后移,指到了元素3,3
复制代码
④ j 一路后移,没有再碰到比主元4小的元素:
复制代码
⑤ 最后,A[i + 1] A[r],即8与4交换,所以,数组最终变成了如下形式:
复制代码
ok,至此快速排序第一趟完成。就这样,4把整个数组分成了俩部分,2 1 3,7 5 6 8,再递归对这俩部分分别进行排序。
全部过程可以参看此文:快速排序算法,或看下我以前在学校里画的图:

而我们面对的问题是,重新排列使得所有球排列成三个不同颜色的球,是否可以设定三个指针,借鉴partition过程呢?
解法一、partition分治
通过前面的分析得知,这个问题,类似快排中partition过程。只是需要用到三个指针,一前begin,一中current,一后end,俩俩交换。
current遍历,整个数组序列,current指1不动,current指0,与begin交换,而后current++,begin++,current指2,与end交换,而后,current不动,end--。
为什么,第三步,current指2,与end交换之后,current不动了列,对的,正如algorithm__所说:current之所以与begin交换后,current++、begin++,是因为此无后顾之忧。而current与end交换后,current不动,end--,是因有后顾之忧。
读者可以试想,你最终的目的无非就是为了让0、1、2有序排列,试想,如果第三步,current与end交换之前,万一end之前指的是0,而current交换之后,current此刻指的是0了,此时,current能动么?不能动啊,指的是0,还得与begin交换列。
ok,说这么多,你可能不甚明了,直接引用下gnuhpc的图,就一目了然了:
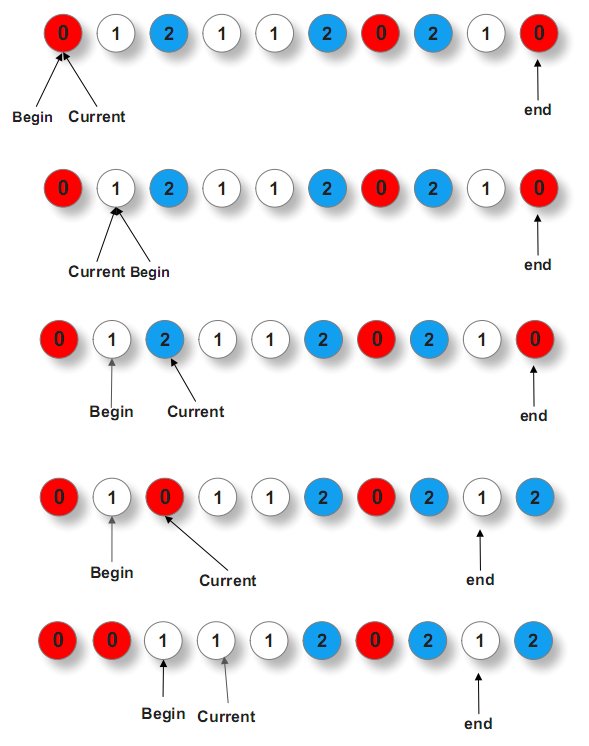
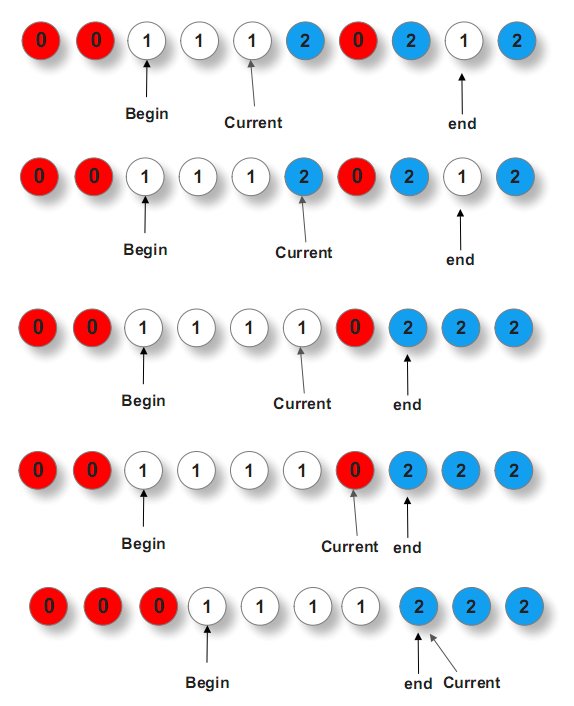
参考代码如下:
- //引用自gnuhpc
- while( current<=end )
- {
- if( array[current] ==0 )
- {
- swap(array[current],array[begin]);
- current++;
- begin++;
- }
- else if( array[current] == 1 )
- {
- current++;
- }
-
- else //When array[current] =2
- {
- swap(array[current],array[end]);
- end--;
- }
- }
本章完。

矩阵相乘之Strassen算法
题目描述
请编程实现矩阵乘法,并考虑当矩阵规模较大时的优化方法。
思路分析
根据wikipedia上的介绍:两个矩阵的乘法仅当第一个矩阵B的列数和另一个矩阵A的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵,它们的乘积AB是一个m×p矩阵,它的一个元素
1TYLX~[{{N`7OF0LIC`M3.tmp[/img]
其中 1 ≤ i ≤ m, 1 ≤ j ≤ p。
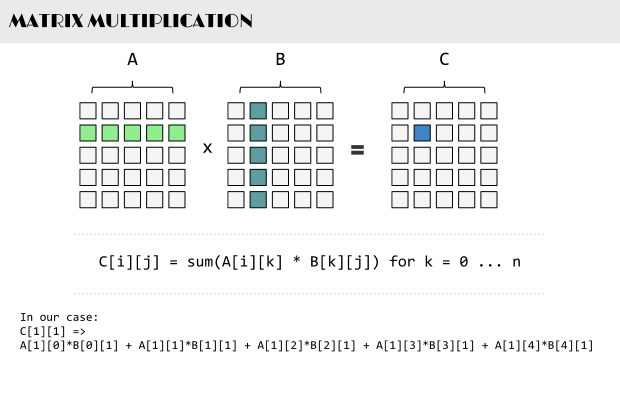
值得一提的是,矩阵乘法满足结合律和分配率,但并不满足交换律,如下图所示的这个例子,两个矩阵交换相乘后,结果变了:

下面咱们来具体解决这个矩阵相乘的问题。
解法一、暴力解法
其实,通过前面的分析,我们已经很明显的看出,两个具有相同维数的矩阵相乘,其复杂度为O(n^3),参考代码如下:
- //矩阵乘法,3个for循环搞定
- void Mul(int** matrixA, int** matrixB, int** matrixC)
- {
- for(int i = 0; i < 2; ++i)
- {
- for(int j = 0; j < 2; ++j)
- {
- matrixC[i][j] = 0;
- for(int k = 0; k < 2; ++k)
- {
- matrixC[i][j] += matrixA[i][k] * matrixB[k][j];
- }
- }
- }
- }
解法二、Strassen算法
在解法一中,我们用了3个for循环搞定矩阵乘法,但当两个矩阵的维度变得很大时,O(n^3)的时间复杂度将会变得很大,于是,我们需要找到一种更优的解法。
一般说来,当数据量一大时,我们往往会把大的数据分割成小的数据,各个分别处理。遵此思路,如果丢给我们一个很大的两个矩阵呢,是否可以考虑分治的方法循序渐进处理各个小矩阵的相乘,因为我们知道一个矩阵是可以分成更多小的矩阵的。
如下图,当给定一个两个二维矩阵A B时:
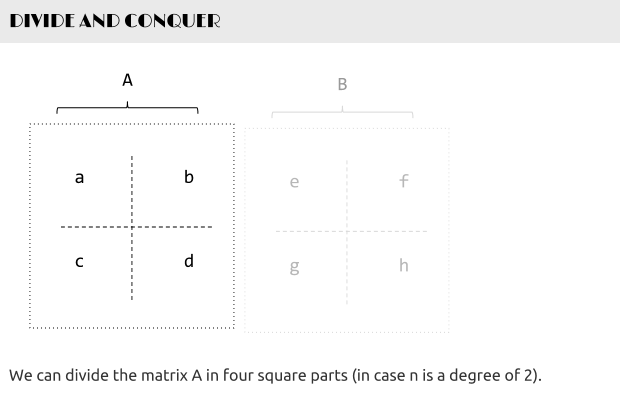
这两个矩阵A B相乘时,我们发现在相乘的过程中,有8次乘法运算,4次加法运算:

矩阵乘法的复杂度主要就是体现在相乘上,而多一两次的加法并不会让复杂度上升太多。故此,我们思考,是否可以让矩阵乘法的运算过程中乘法的运算次数减少,从而达到降低矩阵乘法的复杂度呢?答案是肯定的。
1969年,德国的一位数学家Strassen证明O(N^3)的解法并不是矩阵乘法的最优算法,他做了一系列工作使得最终的时间复杂度降低到了O(n^2.80)。
他是怎么做到的呢?还是用上文A B两个矩阵相乘的例子,他定义了7个变量:

如此,Strassen算法的流程如下:
两个矩阵A B相乘时,将A, B, C分成相等大小的方块矩阵:
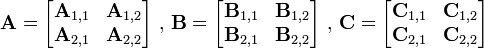
;
可以看出C是这么得来的:
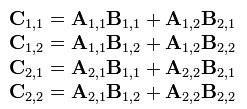
现在定义7个新矩阵(读者可以思考下,这7个新矩阵是如何想到的):

而最后的结果矩阵C 可以通过组合上述7个新矩阵得到:
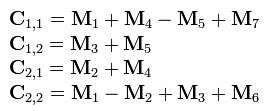
表面上看,Strassen算法仅仅比通用矩阵相乘算法好一点,因为通用矩阵相乘算法时间复杂度是
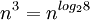
,而Strassen算法复杂度只是
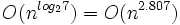
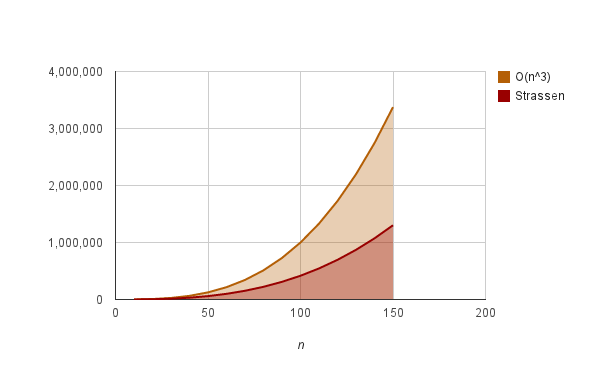
。但随着n的变大,比如当n >> 100时,Strassen算法是比通用矩阵相乘算法变得更有效率。
如下图所示:
解法三、持续优化
根据wikipedia上的介绍,后来,Coppersmith–Winograd 算法把 N* N大小的矩阵乘法的时间复杂度降低到了:
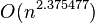
,而2010年,Andrew Stothers再度把复杂度降低到了
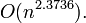
,一年后的2011年,Virginia Williams把复杂度最终定格为:
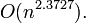
|  /2
/2 