K-means聚类算法

问题导读


1. K-means是什么算法？
2.K-means是如何保证收敛？
3.K-means与EM的关系是什么？

K-means也是聚类算法中最简单的一种了，但是里面包含的思想却是不一般。最早我使用并实现这个算法是在学习韩爷爷那本数据挖掘的书中，那本书比较注重应用。看了Andrew Ng的这个讲义后才有些明白K-means后面包含的EM思想。

     聚类属于无监督学习，以往的回归、朴素贝叶斯、SVM等都是有类别标签y的，也就是说样例中已经给出了样例的分类。而聚类的样本中却没有给定y，只有特征x，比如假设宇宙中的星星可以表示成三维空间中的点集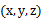。聚类的目的是找到每个样本x潜在的类别y，并将同类别y的样本x放在一起。比如上面的星星，聚类后结果是一个个星团，星团里面的点相互距离比较近，星团间的星星距离就比较远了。

     在聚类问题中，给我们的训练样本是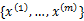，每个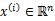，没有了y。

     K-means算法是将样本聚类成k个簇（cluster），具体算法描述如下：

1、 随机选取k个聚类质心点（cluster centroids）为。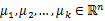

2、 重复下面过程直到收敛 {

               对于每一个样例i，计算其应该属于的类

               

               对于每一个类j，重新计算该类的质心

               

}

     K是我们事先给定的聚类数，代表样例i与k个类中距离最近的那个类，的值是1到k中的一个。质心代表我们对属于同一个类的样本中心点的猜测，拿星团模型来解释就是要将所有的星星聚成k个星团，首先随机选取k个宇宙中的点（或者k个星星）作为k个星团的质心，然后第一步对于每一个星星计算其到k个质心中每一个的距离，然后选取距离最近的那个星团作为，这样经过第一步每一个星星都有了所属的星团；第二步对于每一个星团，重新计算它的质心（对里面所有的星星坐标求平均）。重复迭代第一步和第二步直到质心不变或者变化很小。

     下图展示了对n个样本点进行K-means聚类的效果，这里k取2。

     

     K-means面对的第一个问题是如何保证收敛，前面的算法中强调结束条件就是收敛，可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性，我们定义畸变函数（distortion function）如下：

     

     J函数表示每个样本点到其质心的距离平方和。K-means是要将J调整到最小。假设当前J没有达到最小值，那么首先可以固定每个类的质心，调整每个样例的所属的类别来让J函数减少，同样，固定，调整每个类的质心也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时，和c也同时收敛。（在理论上，可以有多组不同的和c值能够使得J取得最小值，但这种现象实际上很少见）。

     由于畸变函数J是非凸函数，意味着我们不能保证取得的最小值是全局最小值，也就是说k-means对质心初始位置的选取比较感冒，但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优，那么可以选取不同的初始值跑多遍k-means，然后取其中最小的J对应的和c输出。

     下面累述一下K-means与EM的关系，首先回到初始问题，我们目的是将样本分成k个类，其实说白了就是求每个样例x的隐含类别y，然后利用隐含类别将x归类。由于我们事先不知道类别y，那么我们首先可以对每个样例假定一个y吧，但是怎么知道假定的对不对呢？怎么评价假定的好不好呢？我们使用样本的极大似然估计来度量，这里是就是x和y的联合分布P(x,y)了。如果找到的y能够使P(x,y)最大，那么我们找到的y就是样例x的最佳类别了，x顺手就聚类了。但是我们第一次指定的y不一定会让P(x,y)最大，而且P(x,y)还依赖于其他未知参数，当然在给定y的情况下，我们可以调整其他参数让P(x,y)最大。但是调整完参数后，我们发现有更好的y可以指定，那么我们重新指定y，然后再计算P(x,y)最大时的参数，反复迭代直至没有更好的y可以指定。

     这个过程有几个难点，第一怎么假定y？是每个样例硬指派一个y还是不同的y有不同的概率，概率如何度量。第二如何估计P(x,y)，P(x,y)还可能依赖很多其他参数，如何调整里面的参数让P(x,y)最大。这些问题在以后的篇章里回答。

     这里只是指出EM的思想，E步就是估计隐含类别y的期望值，M步调整其他参数使得在给定类别y的情况下，极大似然估计P(x,y)能够达到极大值。然后在其他参数确定的情况下，重新估计y，周而复始，直至收敛。

     上面的阐述有点费解，对应于K-means来说就是我们一开始不知道每个样例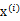对应隐含变量也就是最佳类别。最开始可以随便指定一个给它，然后为了让P(x,y)最大（这里是要让J最小），我们求出在给定c情况下，J最小时的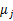（前面提到的其他未知参数），然而此时发现，可以有更好的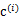（质心与样例距离最小的类别）指定给样例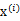，那么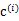得到重新调整，上述过程就开始重复了，直到没有更好的指定。这样从K-means里我们可以看出它其实就是EM的体现，E步是确定隐含类别变量，M步更新其他参数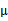来使J最小化。这里的隐含类别变量指定方法比较特殊，属于硬指定，从k个类别中硬选出一个给样例，而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程，有目标函数，也有参数变量，只是多了个隐含变量，确定其他参数估计隐含变量，再确定隐含变量估计其他参数，直至目标函数最优。