层次聚类算法的原理及实现Hierarchical Clustering

问题导读：
1、如何理解层次聚类？
2、如何理解数据点与组合数据点间的距离？
3、如何求得两个组合数据点间的距离？




层次聚类(Hierarchical Clustering)是聚类算法的一种，通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。创建聚类树有自下而上合并和自上而下分裂两种方法，本篇文章介绍合并方法。



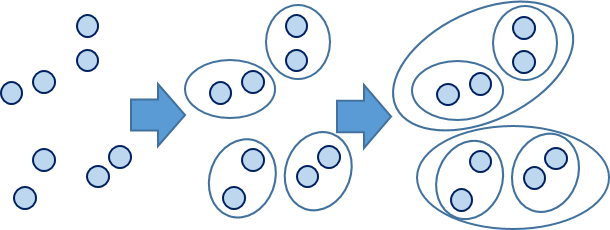
次聚类的合并算法

层次聚类的合并算法通过计算两类数据点间的相似性，对所有数据点中最为相似的两个数据点进行组合，并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性，距离越小，相似度越高。并将距离最近的两个数据点或类别进行组合，生成聚类树。

欧几里德距离矩阵

层次聚类使用欧式距离来计算不同类别数据点间的距离（相似度）。我们在前面的几篇文章中都曾经介绍过欧氏距离的计算方法，本篇文章将通过创建一个欧式距离矩阵来计算和对比不同类别数据点间的距离，并对距离值最小的数据点进行组合。以下是欧式距离的计算公式。


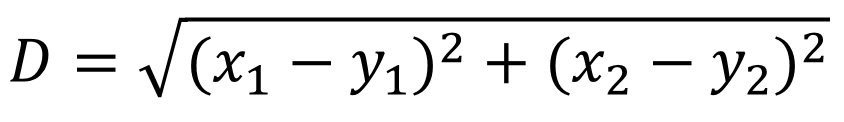
以下为示例数据，我们通过欧氏距离计算下面A到G的欧式距离矩阵，并通过合并的方法将相似度最高的数据点进行组合，并创建聚类树。


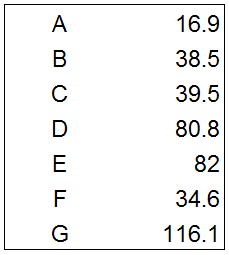
创建欧式距离矩阵的方法很简单，将每个类别的数据点分别与A-G中的每个数据点计算距离值，其中A—>B表示数据点A到数据点B的距离，B—>A则代表数据点B到数据点A的距离。这两个距离值是相同的，因此欧式距离矩阵呈对角线对称（绿色部分和蓝色部分）。其中对角线的0值是数据点与自己的距离值。我们将所有数据点间的距离结果进行对比，选择其中距离最近的两个数据点进行组合，并迭代这一过程。下图显示了欧式矩阵的逻辑和计算方法。


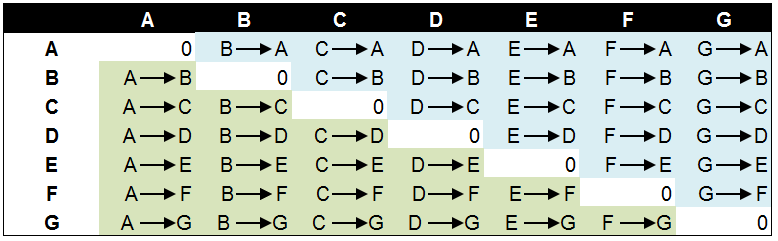
数据点之间的距离   

对于示例中的数据点，我们通过计算获得了下面的欧式距离矩阵。其中数据点B到数据点C的距离在所有的距离值中最小，为1.00。以下为数据点间距离值的计算公式。


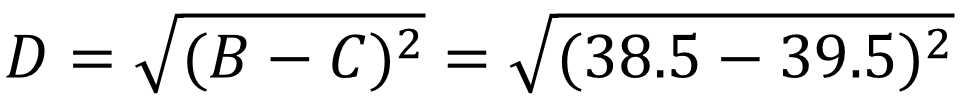
经过计算数据点B和数据点C与其他数据点相比有最高的相似度。因此，我们将数据点B和数据点C进行组合。并再次计算其他数据点间的距离。


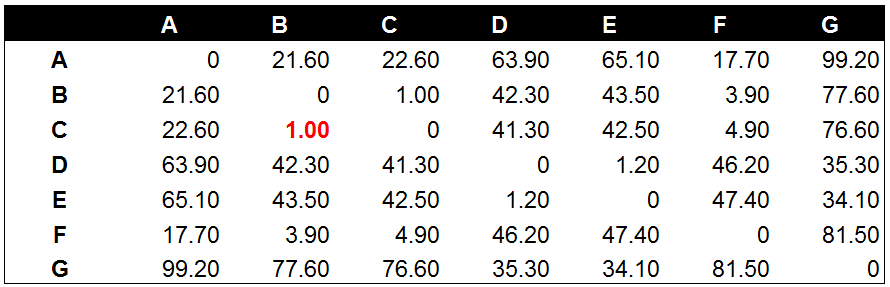
数据点与组合数据点间的距离

将数据点B与数据点C进行组合后，重新计算各类别数据点间的距离矩阵。数据点间的距离计算方式与之前的方法一样。这里需要说明的是组合数据点(B,C)与其他数据点间的计算方法。当我们计算(B,C)到A的距离时，需要分别计算B到A和C到A的距离均值。


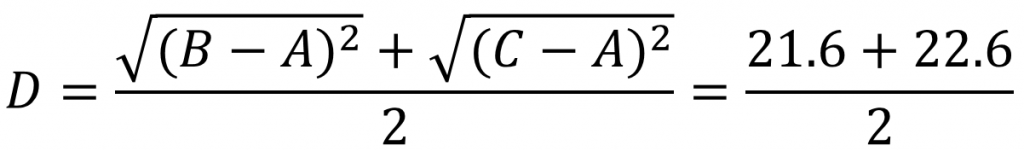
经过计算数据点D到数据点E的距离在所有的距离值中最小，为1.20。这表示在当前的所有数据点中（包含组合数据点），D和E的相似度最高。因此我们将数据点D和数据点E进行组合。并再次计算其他数据点间的距离。


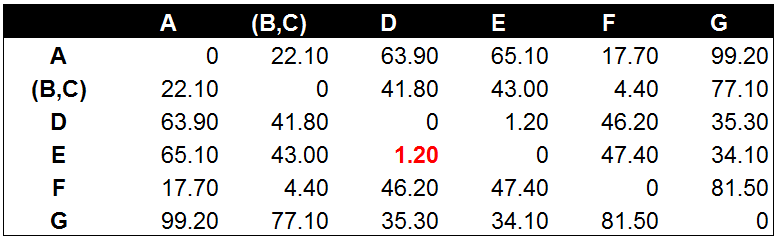
后面的工作就是不断的重复计算数据点与数据点，数据点与组合数据点间的距离。这个步骤应该由程序来完成。这里由于数据量较小，我们手工计算并列出每一步的距离计算和数据点组合的结果。

这一步中，数据点A和数据点F的距离值在所有距离值中最小，因此我们将A和F进行组合，生成组合数据点（A,F）。


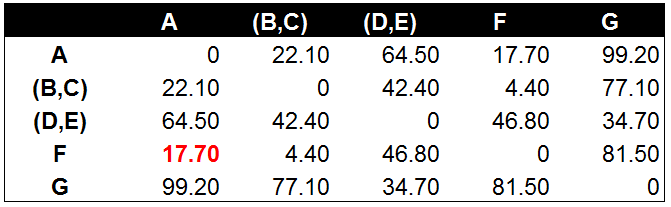
到此为止除了数据点G以外，其他的数据点都已经根据距离值（相似度）进行了组合。聚类树的最底层已经完成。下面我们将继续计算组合数据点间的距离，并对相似度最高的组合数据点进行合并。

两个组合数据点间的距离

计算两个组合数据点间距离的方法有三种，分别为Single Linkage，Complete Linkage和Average Linkage。在开始计算之前，我们先来介绍下这三种计算方法以及各自的优缺点。

• Single Linkage
  

Single Linkage的计算方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个很相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。

• Complete Linkage
  

Complete Linkage的计算方法与Single Linkage相反，将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相反，两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。

• Average Linkage
  

Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大，但结果比前两种方法更合理。

我们使用Average Linkage计算组合数据点间的距离。下面是计算组合数据点(A,F)到(B,C)的距离，这里分别计算了(A,F)和(B,C)两两间距离的均值。


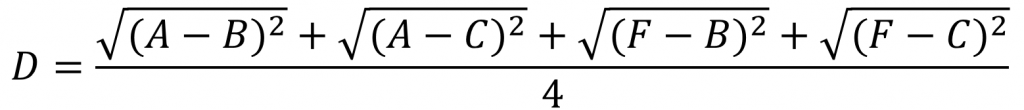
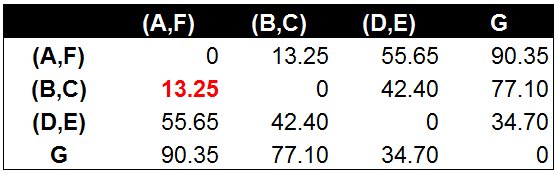
通过计算及对比不同组合数据点间间的距离。(A,F)到(B,C)的距离在所有组合数据点间最小，为13.25。说明(A,F)到(B,C)相似度最高。因此，将(A,F)到(B,C)组合为(A,F,B,C)。


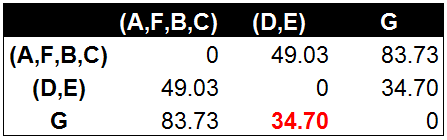
使用与之前相同的方法计算出组合数据点(D,E)和G的距离在目前所有组合数据点中最小。为34.70。将(D,E)和G组合为(D,E,G)。


最终，通过计算和合并，我们获得了两个组合数据点(A,F,B,C)和(D,E,G)。这也是聚类树的最顶层的两个数据点。下面，我们按之前的计算步骤来构建聚类树。


层次聚类树状图

将前面的每一步的计算结果以树状图的形式展现出来就是层次聚类树。最底层是原始A到G的7个数据点。依照7个数据点间的相似度组合为聚类树的第二层(A,F),(B,C),(D,E)和G。以此类推生成完整的层次聚类树状图。以下为简单的示意图。


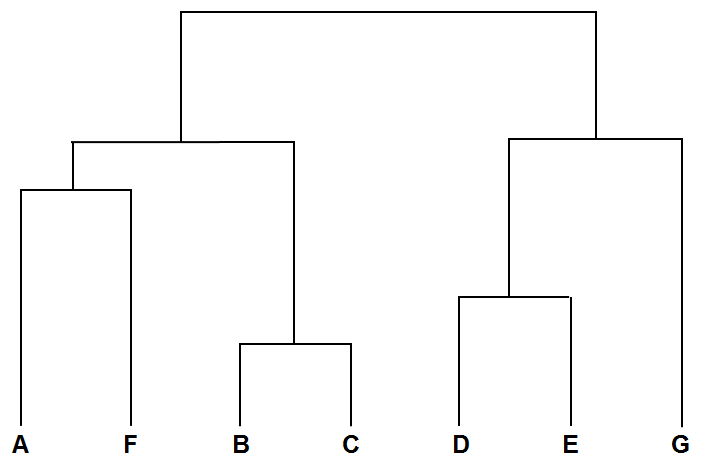
来源：蓝鲸网站分析博客

学习了,写的很好,很容易理解

顶顶顶顶顶顶顶顶顶顶顶顶