使用keras实现deepFM实践

问题导读：
1、如何理解FM 的基本原理？
2、如何做好特征索引？
3、如何实现 deep 部分？
4、如何完整的实现FM代码？





一些前面说明

•     实现基本完全基于文末列出的deepFM 原文（还有几处或者更多地方可以优化，比如二次项多值输入的处理，样本编码等等）
•     文末参考的文章用Keras实现一个DeepFM 是我们初期学习和搭建deepFM 的主要参考。然后下面我们的实现会比参考内容更简单而且有一些处理上的差异。同时在我们的业务数据集上，下面我们自己的实现方式得到的测试 auc 大约都比按照上面文章的实现测试 auc 高约 0～0.01 左右。（当然这里可能有各种原因导致的差异，并不能说下面的实现是绝对优于参考文章的）
•     下面的内容完全是个人行为，有错漏希望多指教
  

实现这个 deepFM 需要掌握的内容

•     Keras 的使用，包括如果使用 Sequential 搭建模型，以及如何使用函数式 API 搭建较简单模型
•     Dense, Embedding, Reshape, Concatenate, Add, Substract, Lambda 这几个 Layer 的使用方式
•     自定义简单的 Layer
  

FM 的基本原理

    另外一些零散又没法绕过的内容（优化器，激活函数，损失函数，正则化），幸运的是这些内容大部分框架帮我们处理好了，我们暂时只需要调参即可，甚至不会调参的化，copy一下别人的配置个人觉得也无伤大雅（毕竟我也只会copy）。这里的参数只要不是太过分，参数变化对对模型结果应该起不到决定性作用。

DeepFM 简述

deepFM 的发展史我们也不多介绍，目前我们也主要用于做 ctr cvr 预测。


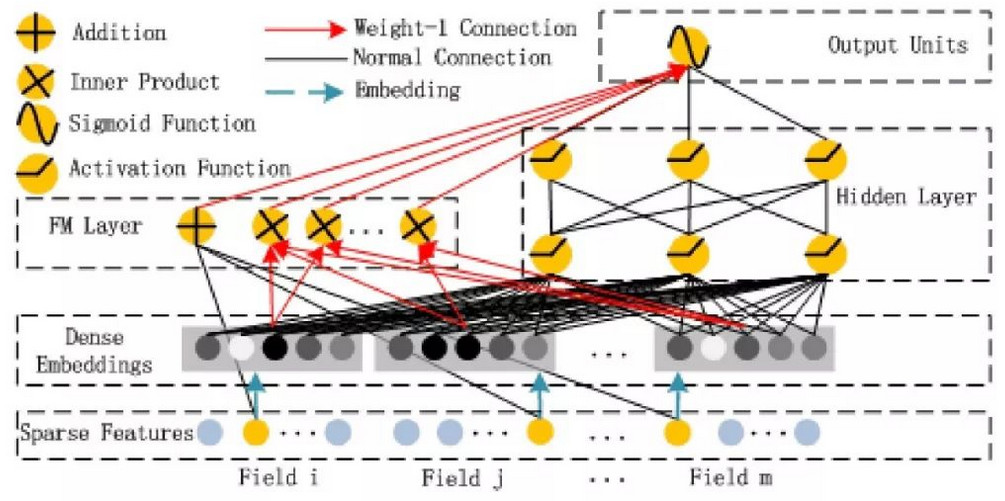
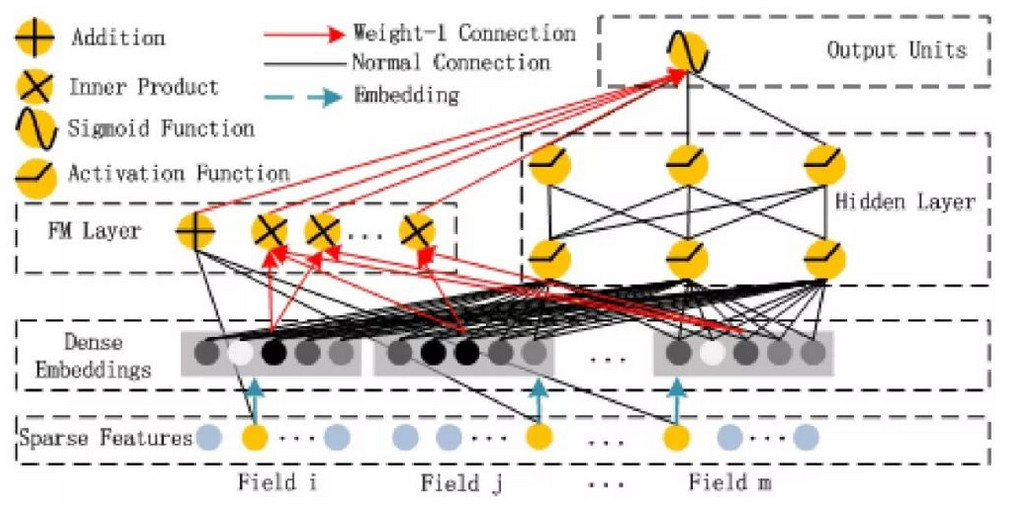
deepFM 说起来结构还是比较简单，包含了左边的 FM 和右边的 deep 部分，每个神经元进行了什么操作也在图中表示得很清楚。需要注意的是，图中的连线有红线和黑线的区别，红线表示权重为 1，黑线表示有需要训练的权重连线。

•     Addition 普通的线性加权相加，就是 w*x
•     Inner Product 内积操作，就是 FM 的二次项隐向量两两相乘的部分
•     Sigmoid 激活函数，即最后整合两部分输出合并进入 sigmoid 激活函数得到的输出结果
•     Activation Function，这里为激活函数用的就是线性整流器 relu 函数
  

FM（因式分解机） 简述

这里不着重描述 FM 是什么，FM 由如下公式表示（只讨论二阶组合的情况）

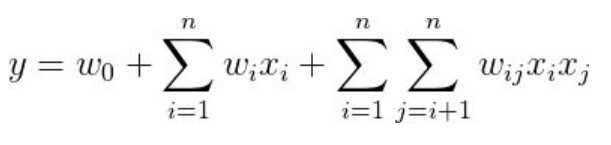
同样是线性公式，和 LR 的唯一区别，就在于后面的二次项，该二次项表示各个特征交叉相乘，即相当于我们在机器学习中的组合特征。

FM 的这部分能力，解决了 LR 只能对一阶特征做学习的局限性。

LR 如果要使用组合特征，必须手动做特征组合，这一步需要经验。FM 的二次项可以自动对特征做组合。

同时 FM 的公式可以化为如下，v 表示的就是对应的特征 x 的隐向量。

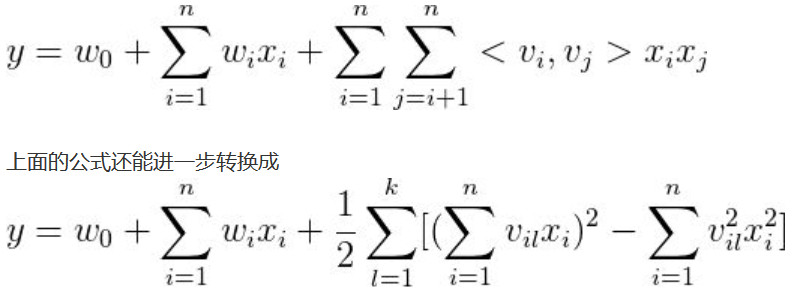
这个公式的优点在于，上一个公式要训练组合权重 w，需要两个组合特征的样本值同时有值才能使 w 得到训练，但是组合特征原本样本就较少，这样的训练方式很难使权重 w 得到充分训练。

通过因式分解机，可以使用一个长度为 k 的隐向量来表达每一个输入的特征值 x，标记为 v，并且通过两个特征的 v 值求内积，其结果可以等同于特征交叉项的权重 w。

通过隐向量 v 表示特征的方式好处是，交叉项不需要保证两个特征均有值才能使 v 得到训练，每一个包含有值特征 x 的样本，都能使之对应的隐向量 v 得到训练。

这里圈一下重点：

•     LR 的升级版
•     有个二阶项（也可以有更高阶项，但付出的计算代价也更大）
•     通过引入隐向量，训练时二阶项组合特征无需同时有值就可以得到训练
  

样本格式

样本保存格式

每个训练样本都会有自己的保存格式，libsvm 或者 tfrecord 或者其他什么形式。

我们的样本格式为：

•     单值离散特征而是直接输入index
•     多值离散特征也是输入 index，但是是输入一串对应的 index 值，如 [5,9,11]
•     如果有没有维表的字符串特征，我们通过哈希转换成某个范围内的数字，这个转换是确定的，比如 “hello” 恒转换成 10，即变成了 1 情况里描述的单值离散特征 （哈希是会出现一定概率碰撞的，这里需要将维度冗余大约10倍使碰撞率低于5%，目前这样处理在我们的场景下模型效果无差异）
•     连续值直接输入即可。（如果是较大的连续值，需在特征工程部分先做归一化，或者考虑先做离散化处理成离散值）
  

最后得到的样本形如 1,5,10,3,6,0.5,0.4,100,[5,9,11]。这样的话，线上的 TFserving 除了最后的 [5,9,11] 部分因为是变长，还是必须转换成 one-hot 形式。其余部分线上交给 embedding 层处理，就无需拼接 one-hot 向量输入，节省输入样本长度。

特征索引

当然如果保存后的样本是上面些的 1,5,10,3,6,0.5,0.4,100,[5,9,11]，我们还需要知道每个值是什么特征，维度是多少，以及训练时如何转换成可以使用的样本。

所以需要有一行特征索引和每一条样本的每个值一一对应。假设可以用以下形式存储索引。

    1-age-100, 1-gender-3, 2-ads_weight-1, 3-game-50...   
     
    对应的每个表示是   
    类型-特征名-维度

左滑查看完整代码，下同

总之只要有一个对应方式，通过查询索引找到特征的信息即可，我们后面的输入样本就需要根据这些信息来转换，并且喂给模型做训练。

模型输入

后续对于模型的输入，我们根据不同特征定义了对应不同的 Input。所以最后输入的训练格式要注意。训练输入应该长相如下，
[mw_shl_code=python,true]
    train_x = [np.array([...]), np.array([...]), np.array([...])]   
    label = np.array([0, 1, 0 ...])[/mw_shl_code]

    实现 FM 部分

谈到具体如何实现模型。下图是 deepFM 网络的 FM 部分。

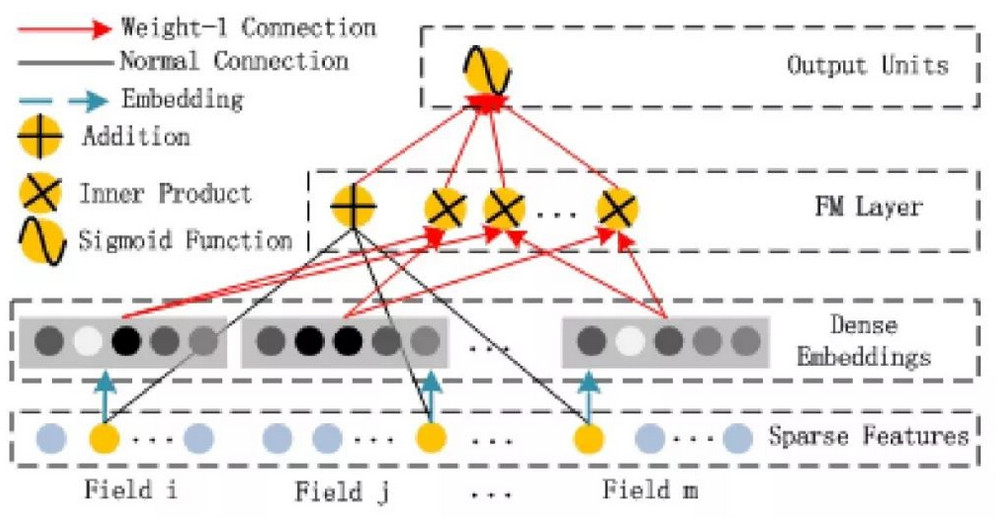
我们看到上图有红色的连线和黑色的连线

•     第一层到第三层的黑色的连线部分就是原始输入通过线性加权，得到模型的一次项。
•     第二层到第三层的红色连线则指的是原始特征通过各自的隐向量来表达后，根据公式两两做内积，得到一堆内积结果
•     最后第三层到第四层的一次项和二次项通过红色连线相加，得到最后的 FM 输出
  

按步骤实现，就是需要实现一次项和二次项两部分，然后相加得到 FM 这部分的输出。

一次项部分
FM 的一次项部分

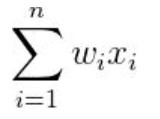
这一部分思路很简单

•     连续值，通过 dense(1) 得到 input*weight 的输出。
•     单值离散特征，通过 embedding(dim,1) 得到一维输出， embedding(dim,1) 可以认为就是 input*weight 得到的一个输出
•     多值离散特征，通过 dense(1) 得到一个输出值，比如 [1,5,7] 实际进入训练时是 [0,1,0,0,0,1,0,1]（假设最大特征就是7）dense(1) 得到的就是对应 1 值乘以 weight并且相加得到的结果。
•     最后把上面1，2，3得到的单位输出全部 Add 相加，得到的就是上述一次项结果。
  

上述过程可以简单通过代码表达为

[mw_shl_code=python,true]    continuous = Input(shape=(1, ), name='single_continuous')   
    single_discrete = Input(shape=(1, ), name='single_discrete')   
    multi_discrete = Input(shape=(8, ), name='multi_discrete')   
    continuous_dense = Dense(1)(continuous)   
    single_embedding = Reshape([1])(Embedding(10, 1)(single_discrete))   
    multi_dense = Dense(1)(multi_discrete)   
    first_order_sum = Add()([continuous_dense, single_embedding, multi_dense])[/mw_shl_code]

二次项部分
FM 的二次项部分

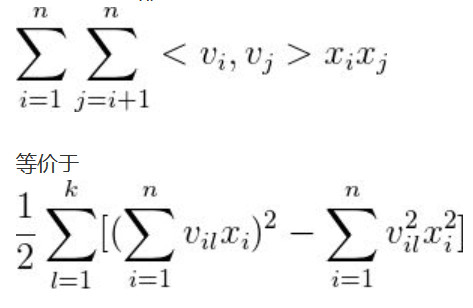
这一部分主要做的事情，就是需要得到一个表示各 field 的隐向量，而且不管每个特征 field 长度是多少，最后得到的隐向量长度都为 k（这里 k 由开发者自己指定）。我们来分析一下如何处理这部分。

•     连续值，要得到 k 长度输出，我们直接使用 dense(k)
•     单值离散特征，同样通过 Embedding(dim,k) 得到 k 长度输出
•     多值离散特征，使用 Dense(k) 得到 k 长度输出（这一部分为了简化，直接使用全连接层，包括后面的二次项操作）。
  

承接上面的代码，这一部分的代码表示为

[mw_shl_code=python,true]    continuous_k = Dense(3)(continuous)   
    single_k = Reshape([3])(Embedding(10, 3)(single_discrete))   
    multi_k = Dense(3)(multi_discrete)[/mw_shl_code]

最后得到如下图的输出，我们这里假设 k=3，下列每一种类型的 3 位输出，最后 concate 在一起，要作为后面说到的 deep 层的输入。


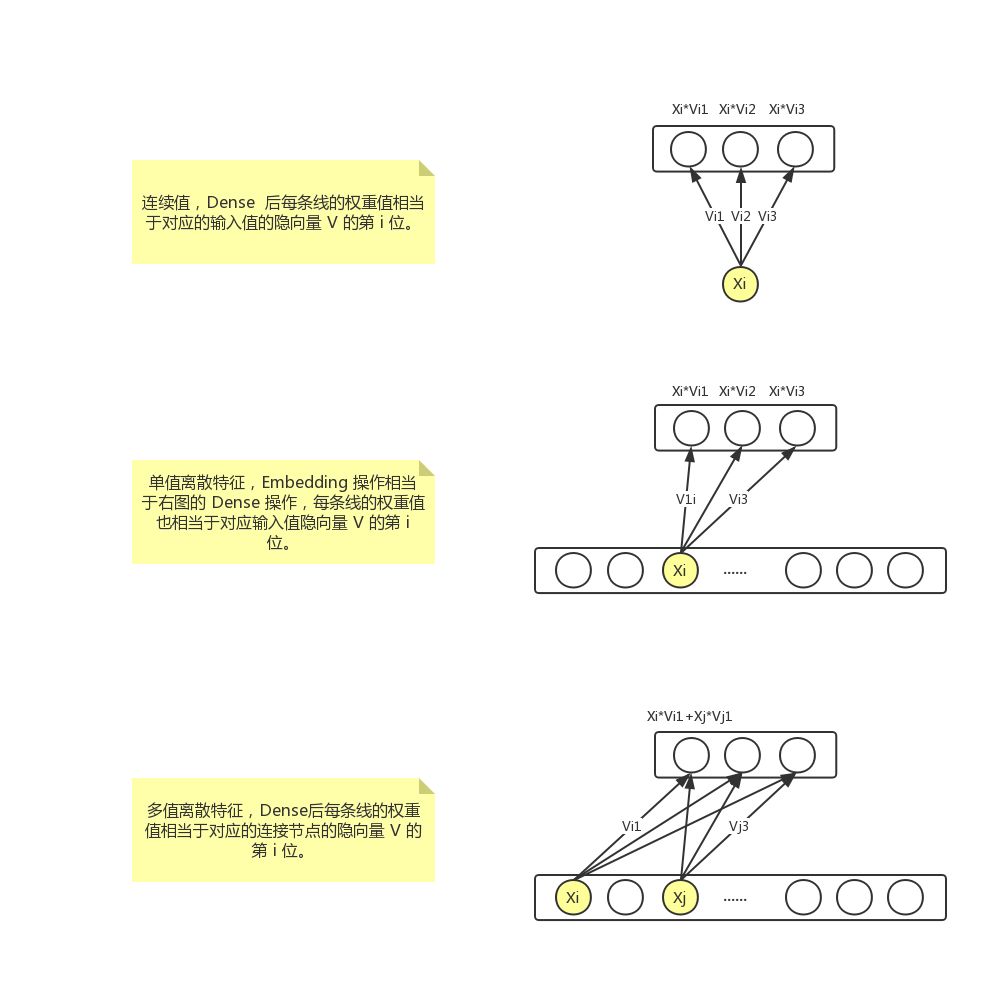
这一部分是先平方后相加

从上一张图我们看到一个信息，每个 k=3 的时候，每个输出节点，其实就相当于 Xi*Vil。

多值离散特征的 k=3 的每个输出其实等于 XiVil+XjVjl，因为他还是同一个 field 的多个特征值，为了简化，我们认为这个结果近似等于

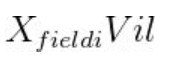
所以不管是要先相加后平方，或者先平方后相加，最后等同于上面的 3 个 3维神经元相加起来，对应得到的数就等于求和部分。如下图。

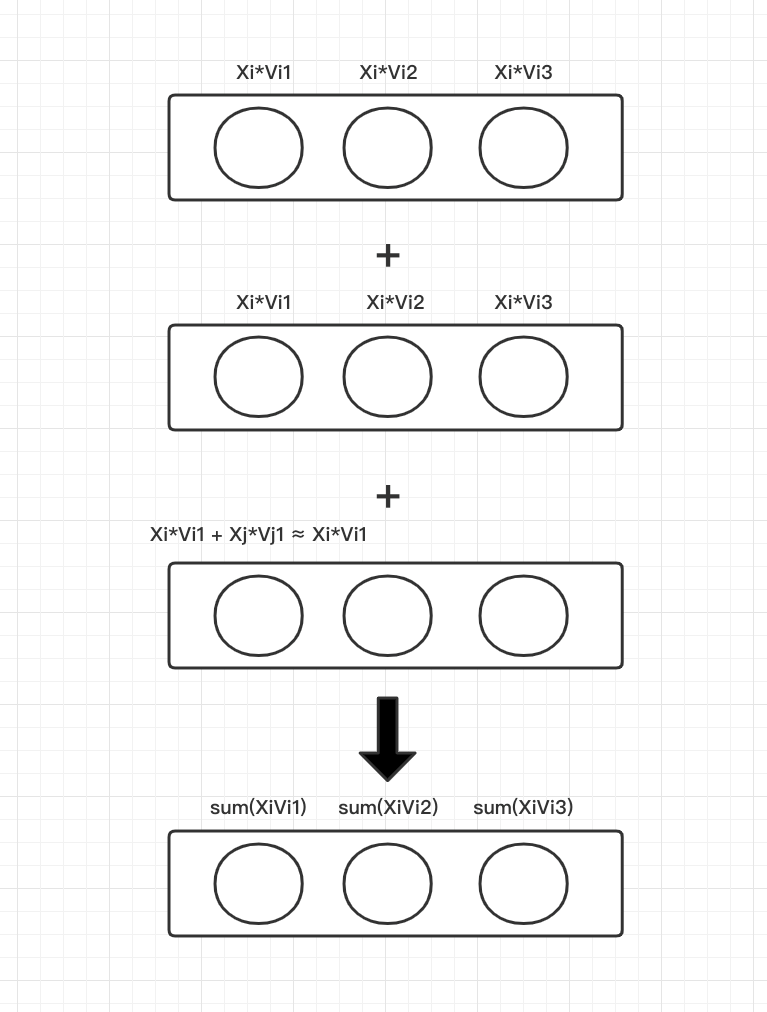
先相加后平方

所以这里每个 k=3 的输出，都是一个 Xi*Vil。先相加后平方的一项，利用 Lambda 层对每个元素做一次平方处理，接上面的代码得到
[mw_shl_code=python,true]
sum_square_layer = Lambda(lambda x: x**2)(Add()([continuous_k, single_k, multi_k]))[/mw_shl_code]

先平方后相加

跟上一步类似，我们得到

[mw_shl_code=python,true]    continuous_square = Lambda(lambda x:x**2)(continuous_k)   
    single_square = Lambda(lambda x:x**2)(single_k)   
    multi_square = Lambda(lambda x:x**2)(multi_k)   
    square_sum_layer = Add()([continuous_square, single_square, multi_square])[/mw_shl_code]

二次项的最后输出

最后结合上面两部分，得到二次项的最后输出为上面两项相减，乘以二分之一后，再对 k=3 的三个值相加。

[mw_shl_code=python,true]   substract_layer = Lambda(lambda x:x*0.5)(Subtract()([sum_square_layer, square_sum_layer]))   
    # 要实现单层的各个值相加，目前 Keras 似乎没有这样的操作   
    # 可以通过自定义一个简单层来简单实现我们需要的功能   
    class SumLayer(Layer):   
      def __init__(self, **kwargs):   
        super(SumLayer, self).__init__(**kwargs)   
      def call(self, inputs):   
        inputs = K.expand_dims(inputs)   
        return K.sum(inputs, axis=1)   
      def compute_output_shape(self, input_shape):   
        return tuple([input_shape[0], 1])   
    # 最后相加 k 维输出，结果等于   
    second_order_sum = SumLayer()(substract_layer)[/mw_shl_code]

FM部分的最后输出
我们再回顾一下要注意到最开始的deepFM论文中的原图，FM 部分最后连接到outpu units的 FM 部分，是红色的线，weight-1 connection。

也就是说，FM 部分最后相当于需要把一次项和二次项的输出值相加得到一个单值输出，然后再跟 deep 部分的输出相加，进入 sigmoid 激活函数。所以 FM 部分我们最后的输出为

[mw_shl_code=python,true]fm_output = Add()([first_order_sum, second_order_sum])[/mw_shl_code]

实现 deep 部分

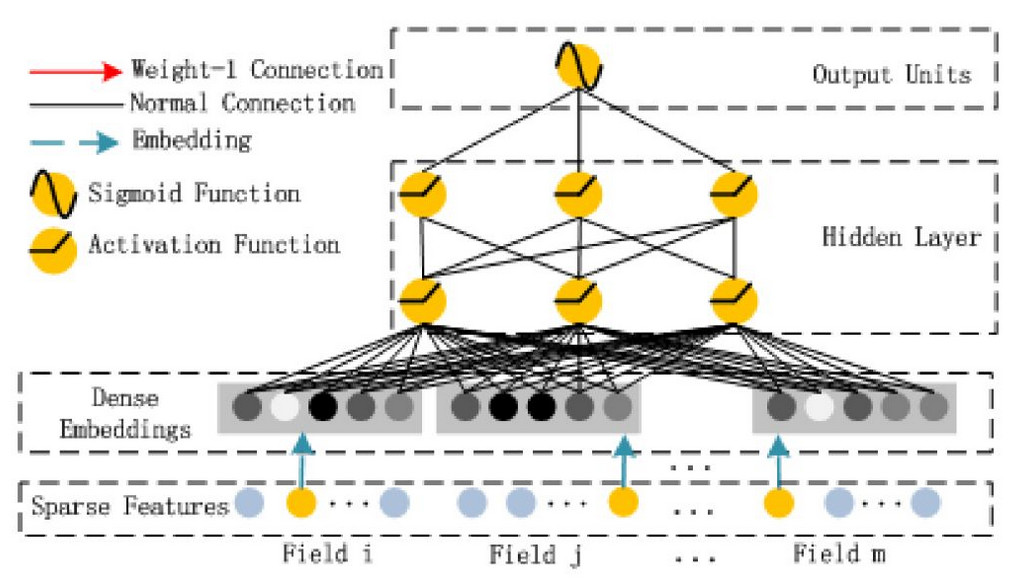
[ deep部分 ]

deep 部分全是黑色连线，所以实现很简单，只需要把上面 FM 部分的二次项 k 维输出 concate 后作为输入，然后进入几层全连接层，最后得到的单值输出和 FM 部分的单值输出 concate，再经过一次 Dense(1)，进入 sigmoid 函数即可。

可以直接看代码如何实现这部分。

[mw_shl_code=python,true]    deep_input = Concatenate()([continuous_k, single_k, multi_k])   
    deep_layer_0 = Dropout(0.5)(Dense(64, activation='relu')(deep_input))   
    deep_layer_1 = Dropout(0.5)(Dense(64, activation='relu')(deep_layer_0))   
    deep_layer_2 = Dropout(0.5)(Dense(64, activation='relu')(deep_layer_1))   
    deep_output = Dropout(0.5)(Dense(1, activation='relu')(deep_layer_2))[/mw_shl_code]

    最后输出部分
[mw_shl_code=python,true]
    concat_layer = Concatenate()([fm_output, deep_output])   
    y = Dense(1, activation='sigmoid')(concat_layer)[/mw_shl_code]

到此模型的代码就完成了，剩余的就是样本的处理，以及各自如何把样本喂入模型的代码。这些代码应该是根据各自业务，各自样本格式需要做对应处理。

deepFM 结果对比

根据上面的方法实现了模型之后，我们用自己的业务的几份数据集做了离线测试。

完整deepFM模型

    只有deep的模型，deep部分的输入是特征简单embedding等处理后的输入，即上面的[continuous_dense, single_embedding, multi_dense] concat后的输入
    只有 FM 的模型，即把 deep 部分去掉，最后进入 Dense(1) 的只有fm_output

在目前我们个业务的几份不同日期的数据集合上测试，得到的AUC 结果如下。

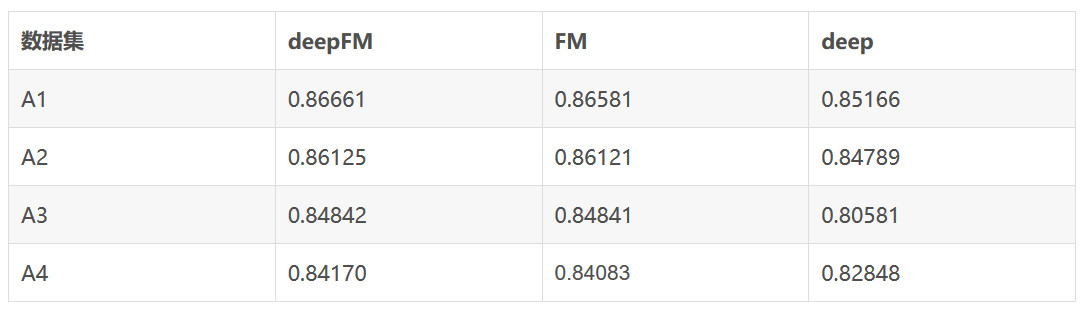
有一个大致经验，deepFM 在有效特征更多，特征工程处理更好，数据更干净，数据更有区分度的数据集上，得到的对比结果差异会更大。

反之，如果数据特征和 label 本身的关联性不高，数据本身无法很好的区分样本时，对比结果差异会很小。

FM 有时候表现已经和 deepFM 几乎无差别。猜测的原因是数据本身并不需要复杂规则就能得到很好的模型区分，所以比 FM 多出来的这部分 deep 能力显得并不太重要。

同时因为 deep 部分明显效果都不如前两者，所以可能可以验证上一步猜测。

预计需要的是更多在特征工程上做优化，以及挖掘更多有效特征。

最后附上代码demo

以上面的代码为例，附上完整的实现代码。这个demo是直接可运行的。

[mw_shl_code=python,true]    import numpy as np   
    from keras.layers import *   
    from keras.models import Model   
    from keras import backend as K   
    from keras import optimizers   
    from keras.engine.topology import Layer   
    # 样本和标签，这里需要对应自己的样本做处理   
    train_x = [   
        np.array([0.5, 0.7, 0.9]),   
        np.array([2, 4, 6]),   
        np.array([[0, 1, 0, 0, 0, 1, 0, 1], [0, 1, 0, 0, 0, 1, 0, 1],   
                  [0, 1, 0, 0, 0, 1, 0, 1]])   
    ]   
    label = np.array([0, 1, 0])   
    # 输入定义   
    continuous = Input(shape=(1, ), name='single_continuous')   
    single_discrete = Input(shape=(1, ), name='single_discrete')   
    multi_discrete = Input(shape=(8, ), name='multi_discrete')   
    # FM 一次项部分   
    continuous_dense = Dense(1)(continuous)   
    single_embedding = Reshape([1])(Embedding(10, 1)(single_discrete))   
    multi_dense = Dense(1)(multi_discrete)   
    # 一次项求和   
    first_order_sum = Add()([continuous_dense, single_embedding, multi_dense])   
    # FM 二次项部分 k=3   
    continuous_k = Dense(3)(continuous)   
    single_k = Reshape([3])(Embedding(10, 3)(single_discrete))   
    multi_k = Dense(3)(multi_discrete)   
    # 先相加后平方   
    sum_square_layer = Lambda(lambda x: x**2)(   
        Add()([continuous_k, single_k, multi_k]))   
    # 先平方后相加   
    continuous_square = Lambda(lambda x: x**2)(continuous_k)   
    single_square = Lambda(lambda x: x**2)(single_k)   
    multi_square = Lambda(lambda x: x**2)(multi_k)   
    square_sum_layer = Add()([continuous_square, single_square, multi_square])   
    substract_layer = Lambda(lambda x: x * 0.5)(   
        Subtract()([sum_square_layer, square_sum_layer]))   
    # 定义求和层   
    class SumLayer(Layer):   
      def __init__(self, **kwargs):   
        super(SumLayer, self).__init__(**kwargs)   
      def call(self, inputs):   
        inputs = K.expand_dims(inputs)   
        return K.sum(inputs, axis=1)   
      def compute_output_shape(self, input_shape):   
        return tuple([input_shape[0], 1])   
    # 二次项求和   
    second_order_sum = SumLayer()(substract_layer)   
    # FM 部分输出   
    fm_output = Add()([first_order_sum, second_order_sum])   
    # deep 部分   
    deep_input = Concatenate()([continuous_k, single_k, multi_k])   
    deep_layer_0 = Dropout(0.5)(Dense(64, activation='relu')(deep_input))   
    deep_layer_1 = Dropout(0.5)(Dense(64, activation='relu')(deep_layer_0))   
    deep_layer_2 = Dropout(0.5)(Dense(64, activation='relu')(deep_layer_1))   
    deep_output = Dropout(0.5)(Dense(1, activation='relu')(deep_layer_2))   
    concat_layer = Concatenate()([fm_output, deep_output])   
    y = Dense(1, activation='sigmoid')(concat_layer)   
    model = Model(inputs=[continuous, single_discrete, multi_discrete], outputs=y)   
    Opt = optimizers.Adam(   
        lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)   
    model.compile(   
        loss='binary_crossentropy',   
        optimizer=Opt,   
        metrics=['acc'])   
    model.fit(   
        train_x,   
        label,   
        shuffle=True,   
        epochs=1,   
        verbose=1,   
        batch_size=1024,   
        validation_split=None)    [/mw_shl_code]

作者：腾讯技术工程
来源：https://blog.csdn.net/Tencent_TE ... 3341?utm_source=app

感谢分享